Abstract

For a real solution

to the Euler stationary equations for ideal fluid, the speaker and his research group derive an infinite series of identities (orthogonality relations) that equate some linear combinations of mth degree integral momenta of the functions u_iu_j and p to zero (m = 0, 1, ... ). In particular, zeroth degree orthogonality relations are:

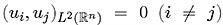and

.

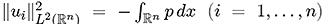Orthogonality relations of degree m are valid for a solution

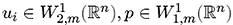, where

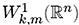 is the weighted Sobolev space with the norm

.

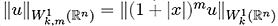About the speaker

Prof Vladimir Sharafutdinov obtained his PhD in Differential Geometry at Novosibirsk State University in 1974 and his Doctor of Sciences at Sobolev Institute of Mathematics in 1990. During 1973 – 1977, he was an Assistant Professor at the Novosibirsk State Pedagogical College. He then moved to the Novosibirsk State University in 1978 and is currently a Professor there. He is also the Leading Researcher at the Sobolev Institute of Mathematics in Novosibirsk.

Prof Sharafutdinov's research interests lie in Riemannian geometry, inverse problems and mathematical problems of tomography.

About the program

For more information, please refer to the program website at http://iasprogram.ust.hk/inverseproblems.

The seminar is free and open to all. Seating is on a first come, first served basis.

HKUST Jockey Club Institute for Advanced Study
Enquiries: ias@ust.hk / 2358 5912
http://ias.ust.hk